给定一个二维网格 grid ,其中:
- ‘.’ 代表一个空房间
- ‘#’ 代表一堵
- ‘@’ 是起点
- 小写字母代表钥匙
- 大写字母代表锁
我们从起点开始出发,一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走,也无法穿过一堵墙。如果途经一个钥匙,我们就把它捡起来。除非我们手里有对应的钥匙,否则无法通过锁。
假设 k 为 钥匙/锁 的个数,且满足 1 <= k <= 6,字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之,每个锁有唯一对应的钥匙,每个钥匙也有唯一对应的锁。另外,代表钥匙和锁的字母互为大小写并按字母顺序排列。
返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙,返回 -1 。
示例 1:
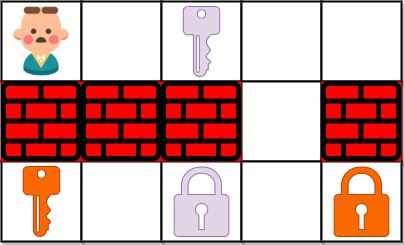
输入:grid = ["@.a.#","###.#","b.A.B"] 输出:8 解释:目标是获得所有钥匙,而不是打开所有锁。
示例 2:
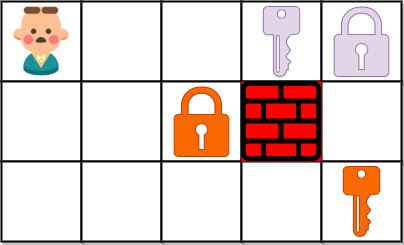
输入:grid = ["@..aA","..B#.","....b"] 输出:6
示例 3:

输入: grid = ["@Aa"] 输出: -1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]只含有'.','#','@','a'-'f'以及'A'-'F'- 钥匙的数目范围是
[1, 6] - 每个钥匙都对应一个 不同 的字母
- 每个钥匙正好打开一个对应的锁
————————————————————————————————————————–
没有能力解决参考了题解
————————————————————————————————————————–
BFS + 状态压缩
一道常规的 BFS 运用题,只不过需要在 BFS 过程中记录收集到的钥匙状态。
利用「钥匙数量不超过 666,并按字母顺序排列」,我们可以使用一个 int 类型二进制数 state 来代指当前收集到钥匙情况:
若 state 的二进制中的第 kkk 位为 1,代表当前种类编号为 kkk 的钥匙 已被收集,后续移动若遇到对应的锁则 能通过
若 state 的二进制中的第 kkk 位为 0,代表当前种类编号为 kkk 的钥匙 未被收集,后续移动若遇到对应的锁则 无法通过
其中「钥匙种类编号」则按照小写字母先后顺序,从 000 开始进行划分对应:即字符为 a 的钥匙编号为 0,字符为 b 的钥匙编号为 1,字符为 c 的钥匙编号为 2 …
当使用了这样的「状态压缩」技巧后,我们可以很方便通过「位运算」进行 钥匙检测 和 更新钥匙收集状态:
钥匙检测:(state >> k) & 1,若返回 1 说明第 kkk 位为 1,当前持有种类编号为 k 的钥匙
更新钥匙收集状态:state |= 1 << k,将 state 的第 kkk 位设置为 1,代表当前新收集到种类编号为 k 的钥匙
搞明白如何记录当前收集到的钥匙状态后,剩下的则是常规 BFS 过程:
起始遍历一次棋盘,找到起点位置,并将其进行入队,队列维护的是 (x,y,state)(x, y, state)(x,y,state) 三元组状态(其中 (x,y)(x, y)(x,y) 代表当前所在的棋盘位置,statestatestate 代表当前的钥匙收集情况) 同时统计整个棋盘所包含的钥匙数量 cnt,并使用 数组/哈希表 记录到达每个状态所需要消耗的最小步数 step
进行四联通方向的 BFS,转移过程中需要注意「遇到锁时,必须有对应钥匙才能通过」&「遇到钥匙时,需要更新对应的 state 再进行入队」
当 BFS 过程中遇到 state = (1 << cnt) – 1 时,代表所有钥匙均被收集完成,可结束搜索
作者:宫水三叶
链接:https://leetcode.cn/problems/shortest-path-to-get-all-keys/solutions/1960544/by-ac_oier-5gxc/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
————————————————————————————————————————–
1 class Solution { 2 static int N = 35, K = 10, INF = 0x3f3f3f3f; 3 static int[][][] dist = new int[N][N][1 << K]; 4 static int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}}; 5 public int shortestPathAllKeys(String[] g) { 6 int n = g.length, m = g[0].length(), cnt = 0; 7 Deque<int[]> d = new ArrayDeque<>(); 8 for (int i = 0; i < n; i++) { 9 for (int j = 0; j < m; j++) { 10 Arrays.fill(dist[i][j], INF); 11 char c = g[i].charAt(j); 12 if (c == '@') { 13 d.addLast(new int[]{i, j, 0}); 14 dist[i][j][0] = 0; 15 } else if (c >= 'a' && c <= 'z') cnt++; 16 } 17 } 18 while (!d.isEmpty()) { 19 int[] info = d.pollFirst(); 20 int x = info[0], y = info[1], cur = info[2], step = dist[x][y][cur]; 21 for (int[] di : dirs) { 22 int nx = x + di[0], ny = y + di[1]; 23 if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue; 24 char c = g[nx].charAt(ny); 25 if (c == '#') continue; 26 if ((c >= 'A' && c <= 'Z') && (cur >> (c - 'A') & 1) == 0) continue; 27 int ncur = cur; 28 if (c >= 'a' && c <= 'z') ncur |= 1 << (c - 'a'); 29 if (ncur == (1 << cnt) - 1) return step + 1; 30 if (step + 1 >= dist[nx][ny][ncur]) continue; 31 dist[nx][ny][ncur] = step + 1; 32 d.addLast(new int[]{nx, ny, ncur}); 33 } 34 } 35 return -1; 36 } 37 } 38 39 作者:宫水三叶 40 链接:https://leetcode.cn/problems/shortest-path-to-get-all-keys/solutions/1960544/by-ac_oier-5gxc/ 41 来源:力扣(LeetCode) 42 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
原文地址:http://www.cnblogs.com/wzxxhlyl/p/16876768.html
